Let’s pause for a moment. Everything that we’ve described so far is just an abstract algorithm for achieving distributed consensus and is not specific to the application. Now we’re going to break out of that model, and we’re going to use the fact that the application we’re building through this
distributed consensus process is in fact a currency. Specifically, we’re going to incentivize nodes to behave honestly by paying them in units of this currency.
Block Reward. How is this done? There are two separate incentive mechanisms in Bitcoin. The first is the block reward. According to the rules of Bitcoin, the node that creates a block gets to include a special transaction in that block. This transaction is a coin‐creation transaction, analogous to CreateCoins in Scroogecoin, and the node can also choose the recipient address of this transaction. Of course that node will typically choose an address belonging to itself. You can think of this as a payment to the node in exchange for the service of creating a block on the consensus chain.
At the time of this writing, the value of the block reward is fixed at 25 Bitcoins. But it actually halves every 210,000 blocks. Based on the rate of block creation that we will see shortly, this means that the rate drops roughly every four years. We’re now in the second period. For the first four years of Bitcoin’s existence, the block reward was 50 bitcoins; now it’s 25. And it’s going to keep halving. This has some interesting consequences, which we will see shortly.
You may be wondering why the block reward incentivizes honest behavior. It may appear, based on what what we’ve said so far, that this node gets the block reward regardless of whether it proposes a valid block or behaves maliciously. But this is not true! Think about it — how will this node “collect” its reward? That will only happen if the block in question ends up on the long‐term consensus branch because just like every other transaction, the coin‐creation transaction will only be accepted by other nodes if it ends up on the consensus chain. That’s the key idea behind this incentive mechanism. It’s a very subtle but very powerful trick. It incentivizes nodes to behave in whatever way they believe will get other nodes to extend their blocks. So if most of the network is following the longest valid branch rule, it incentivizes all nodes to continue to follow that rule. That’s Bitcoin’s first incentive mechanism.
We mentioned that every 210,000 blocks (or approximately four years), the block reward is cut in half. In Figure 2.4, the slope of this curve is going to keep halving. This is a geometric series, and you might know that it means that there is a finite sum. It works out to a total of 21 million bitcoins.
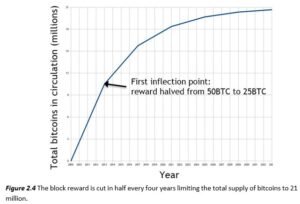
It is important to note that this is the only way in which new bitcoins are allowed to be created. There is no other coin generation mechanism, and that’s why 21 million is a final and total number (as the rules stand now, at least) for how many bitcoins there can ever be. This new block creation reward is actually going to run out in 2140, as things stand now. Does that mean that the system will stop working in 2140 and become insecure because nodes no longer have the incentive to behave honestly? Not quite. The block reward is only the first of two incentive mechanisms in Bitcoin.
Transaction fees The second incentive mechanism is called the transaction fee. The creator of any transaction can choose to make the total value of the transaction outputs less than the total value of its inputs. Whoever creates the block that first puts that transaction into the block chain gets to collect the difference, which acts a transaction fee. So if you’re a node that’s creating a block that contains, say, 200 transactions, then the sum of all those 200 transaction fees is paid to the address that you put into that block. The transaction fee is purely voluntary, but we expect, based on our
understanding of the system, that as the block reward starts to run out, it will become more and more important, almost mandatory, for users to include transaction fees in order to get a reasonable quality of service. To a certain degree, this is already starting to happen now. But it is yet unclear precisely how the system will evolve; it really depends on a lot of game theory which hasn’t been fully worked out yet. That’s an interesting area of open research in Bitcoin.
There are still a few problems remaining with the consensus mechanism as we described it. The first
major one is the leap of faith that we asked you to take that somehow we can pick a random node. Second, we’ve created a new problem by giving nodes these incentives for participation. The system can become unstable as the incentives cause a free‐for‐all where everybody wants to run a Bitcoin node in the hope of capturing some of these rewards. And a third one is an even trickier version of this problem, which is that an adversary might create a large number of Sybil nodes to try and subvert the consensus process.
Mining and proof‐of‐work. It turns out that all of these problems are related, and all of them have the same solution, which is called proof‐of‐work. The key idea behind proof‐of‐work is that we approximate the selection of a random node by instead selecting nodes in proportion to a resource that we hope that nobody can monopolize. If, for example, that resource is computing power, then
it’s a proof‐of‐work system. Alternately, it could be in proportion to ownership of the currency, and that’s called proof‐of‐stake. Although it’s not used in Bitcoin, proof‐of‐stake is a legitimate alternate model and it’s used in other cryptocurrencies. We’ll see more about proof‐of‐stake and other proof‐of‐work variants in Chapter 8.
But back to proof‐of‐work. Let’s try to get a better idea of what it means to select nodes in proportion to their computing power. Another way of understanding this is that we’re allowing nodes to compete with each other by using their computing power, and that will result in nodes automatically being picked in that proportion. Yet another view of proof‐of‐work is that we’re making it moderately hard to create new identities. It’s sort of a tax on identity creation and therefore on the Sybil attack. This might all appear a bit vague, so let’s go ahead and look at the details of the proof‐of‐work system that’s used in Bitcoin, which should make things a lot clearer.
Bitcoin achieves proof‐of‐work using hash puzzles. In order to create a block, the node that proposes that block is required to find a number, or nonce, such that when you concatenate the nonce, the previous hash, and the list of transactions that comprise that block and take the hash of this whole string, then that hash output should be a number that falls into a target space that is quite small in relation to the much larger output space of that hash function. We can define such a target space as any value falling below a certain target value. In this case, the nonce will have to satisfy the following inequality:
H(nonce || prev_hash || tx || tx || … || tx) < target
As we saw earlier, normally a block contains a series of transactions that a node is proposing. In addition, a block also contains a hash pointer to the previous block1. In addition, we’re now requiring that a block also contain a nonce. The idea is that we want to make it moderately difficult to find a nonce that satisfies this required property, which is that hashing the whole block together, including that nonce, is going to result in a particular type of output. If the hash function satisfies the
puzzle‐friendliness property from Chapter 1, then the only way to succeed in solving this hash puzzle is to just try enough nonces one by one until you get lucky. So specifically, if this target space were just one percent of the overall output space, you would have to try about 100 nonces before you got lucky. In reality, the size of this target space is not nearly as high as one percent of the output space. It’s much, much smaller than that as we will see shortly.
This notion of hash puzzles and proof of work completely does away with the requirement to magically pick a random node. Instead, nodes are simply independently competing to solve these hash puzzles all the time. Once in a while, one of them will get lucky and will find a random nonce that satisfies this property. That lucky node then gets to propose the next block. That’s how the system is completely decentralized. There is nobody deciding which node it is that gets to propose the next block.
Difficult to compute. There are three important properties of hash puzzles. The first is that they need to be quite difficult to compute. We said moderately difficult, but you’ll see why this actually varies with time. As of the end of 2014, the difficulty level is about 1020 hashes per block. In other words the size of the target space is only 1/1020 of the size of the output space of the hash function. This is a lot of computation — it’s out of the realm of possibility for a commodity laptop, for example. Because of this, only some nodes even bother to compete in this block creation process. This process of repeatedly trying and solving these hash puzzles is known as Bitcoin mining, and we call the participating nodes miners. Even though technically anybody can be a miner, there’s been a lot of concentration of power in the mining ecosystem due to the high cost of mining.
Parameterizable cost. The second property is that we want the cost to be parameterizable, not a fixed cost for all time. The way that’s accomplished is that all the nodes in the Bitcoin peer‐to‐peer network will automatically recalculate the target, that is the size of the target space as a fraction of the output space, every 2016 blocks. They recalculate the target in such a way that the average time between successive blocks produced in the Bitcoin network is about 10 minutes. With a 10‐minute average time between blocks, 2016 blocks works out to two weeks. In other words, the recalculation of the target happens roughly every two weeks.
Let’s think about what this means. If you’re a miner, and you’ve invested a certain fixed amount of hardware into Bitcoin mining, but the overall mining ecosystem is growing, more miners are coming in, or they’re deploying faster and faster hardware, that means that over a two week period, slightly more blocks are going to be found than expected. So nodes will automatically readjust the target, and the amount of work that you have to do to be able to find a block is going to increase. So if you put in a fixed amount of hardware investment, the rate at which you find blocks is actually dependent upon what other miners are doing. There’s a very nice formula to capture this, which is that the probability that any given miner, Alice, is going to win the next block is equivalent to the fraction of global hash power that she controls. This means that if Alice has mining hardware that’s about 0.1 percent of total hash power, she will find roughly one in every 1,000 blocks.
What is the purpose of this readjustment? Why do we want to maintain this 10‐minute invariant? The reason is quite simple. If blocks were to come very close together, then there would be a lot of inefficiency, and we would lose the optimization benefits of being able to put a lot of transactions in a single block. There is nothing magical about the number 10, and if you went down from 10 minutes to 5 minutes, it would probably be just fine. There’s been a lot of discussion about the ideal block latency that altcoins, or alternative cryptocurrencies, should have. But despite some disagreements about the ideal latency, everybody agrees that it should be a fixed amount. It cannot be allowed to go down without limit. That’s why we have the automatic target recalculation feature.
The way that this cost function and proof of work is set up allows us to reformulate our security assumption. Here’s where we finally depart from the last leap of faith that we asked you to take earlier. Instead of saying that somehow the majority of nodes are honest in a context where nodes don’t even have identities and not being clear about what that means, we can now state crisply, that a lot of attacks on Bitcoin are infeasible if the majority of miners, weighted by hash power, are following the protocol — or, are honest. This is true because if a majority of miners, weighted by hash power, are honest, the competition for proposing the next block will automatically ensure that there is at least a 50 percent chance that the next block to be proposed at any point is coming from an honest node.
Sidebar. in the research fields of distributed systems and computer security, it is common to assume that some percentage of nodes are honest and to show that the system works as intended even if the other nodes behave arbitrarily. That’s basically the approach we’ve taken here, except that we weight nodes by hash power in computing the majority. The original Bitcoin whitepaper contains this type of analysis as well.
But the field of game theory provides an entirely different, and arguably more sophisticated and realistic way to determine how a system will behave. In this view, we don’t split nodes into honest and malicious. Instead, we assume that every node acts according to its incentives. Each node picks a (randomized) strategy to maximize its payoff, taking into account other nodes’ potential strategies. If the protocol and incentives are designed well, then most nodes will follow the rules most of the time. “Honest” behavior is just one strategy of many, and we attach no particular moral salience to it.
In the game theoretic view, the big question is whether the default miner behavior is a “Nash equilibrium,” that is, whether it represents a stable situation in which no miner can realize a higher payoff by deviating from honest behavior. This question is still contentious and an active area of research.
Solving hash puzzles is probabilistic because nobody can predict which nonce is going to result in solving the hash puzzle. The only way to do it is to try nonces one by one and hope that one succeeds. Mathematically, this process is called Bernoulli trials. A Bernoulli trial is an experiment with two
possible outcomes, and the probability of each outcome occurring is fixed between successive trials. Here, the two outcomes are whether or not the hash falls in the target, and assuming the hash functions behaves like a random function, the probability of those outcomes is fixed. Typically, nodes try so many nonces that Bernoulli trials, a discrete probability process, can be well approximated by a continuous probability process called a Poisson process, a process in which events occur independently at a constant average rate. The end result of all of that is that the probability density function that shows the relative likelihood of the time until the next block is found looks like Figure 2.5.
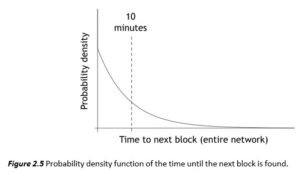
This is known as an exponential distribution. There is some small probability that if a block has been found now, the next block is going to be found very soon, say within a few seconds or a minute. And there is also some small probability that it will take a long time, say an hour, to find the next block. But overall, the network automatically adjusts the difficulty so that the inter‐block time is maintained at an average, long term, of 10 minutes. Notice that Figure 2.5 shows how frequently blocks are going to be created by the entire network not caring about which miner actually finds the block.
If you’re a miner, you’re probably interested in how long it will take you to find a block. What does
this probability density function look like? It’s going to have the same shape, but it’s just going to have a different scale on the x‐axis. Again, it can be represented by a nice equation.
For a specific miner:
mean time to next block = 10 minutes fraction of hash power
If you have 0.1 percent of the total network hash power, this equation tells us that you’re going to find blocks once every 10,000 minutes, which is just about a week. Not only is your mean time between blocks going to be very high, but the variance of the time between blocks found by you is also going to be very high. This has some important consequences that we’re going to look at in chapter 5.
Trivial to verify. Let’s now turn to the third important property of this proof of work function, which is that it is trivial to verify that a node has computed proof of work correctly. Even if it takes a node, on average, 1020 tries to find a nonce that makes the block hash fall below the target, that nonce must be published as part of the block. It is thus trivial for any other node to look at the block contents, hash them all together, and verify that the output is less than the target. This is quite an important
property because, once again, it allows us to get rid of centralization. We don’t need any centralized authority verifying that miners are doing their job correctly. Any node or any miner can instantly verify that a block found by another miner satisfies this proof‐of‐work property.





































